Régression linéaire : comment ça fonctionne ?

La régression linéaire n'est pas qu'une simple équation : c'est la clé qui dévoile les relations entre des variables apparemment disparates. Cette technique statistique façonne les prédictions et les stratégies dans de nombreux secteurs, de l'économie à la technologie, en passant par le marketing.

A quoi sert la régression linéaire ?

La régression linéaire est utilisée par certaines entreprises pour prévoir leurs ventes futures ou par les scientifiques pour prédire les tendances climatiques. Elle revient à trouver la meilleure ligne droite qui passe à travers un ensemble de points sur un graphique. Cette ligne aide à déceler une tendance, à appréhender les relations entre différentes données et également à réaliser des projections.

La régression linéaire est utile pour comprendre comment plusieurs variables interagissent et s'influencent mutuellement. Concrètement, cela permet de savoir si, par exemple, l'augmentation des dépenses publicitaires impacte les ventes ou d'estimer le prix probable d'une maison en fonction de sa taille et de son emplacement.

Il y a plusieurs types de régressions linéaires :

• Linéaire simple (exemple : prévoir le poids d'une personne en fonction de sa taille)
• Linéaire multiple (exemple : estimer le prix d'une voiture en se basant sur sa marque, son modèle et son kilométrage)
• Polynomiale, qui ressemble à une courbe plutôt qu'à une ligne droite (utile dans des cas comme le suivi de la trajectoire d'une balle lancée)
• Exponentielle et Logarithmique, qui sont plus complexes et utilisées pour des situations spécifiques comme la croissance des populations ou certains phénomènes naturels

La régression linéaire est utilisée dans différents domaines :

• En économie (comprendre comment l'emploi et les salaires affectent l'économie globale)
• En marketing (savoir si une nouvelle publicité entraîne plus de ventes)
• En médecine (aider les médecins à comprendre l'efficacité d'un nouveau médicament)
• En écologie (suivre comment les populations animales changent avec le temps)

Comment fonctionne la régression linéaire ?

La relation entre 2 éléments

Pour comprendre le fonctionnement d'une régression linéaire, il est utile de prendre un exemple, comme calculer si les heures passées à étudier influencent la note à un examen. La régression linéaire simple interprète cette relation en dessinant une ligne droite. Elle utilise une formule comme celle-ci :

Note = point de départ + effet de l'étude + marge d'erreur

1. Le point de départ (ou ordonnée à l'origine) : c'est la note qui aurait été probablement obtenue sans aucune heure d'étude. Sur le graphique, c'est là où la ligne touche l'axe vertical.
2. L'effet de l'étude (ou pente) : c'est l'élément clé qui établit de combien la note augmente (ou diminue) pour chaque heure supplémentaire d'étude. Si la pente est positive, cela signifie qu'étudier davantage pourrait aider à obtenir une meilleure note.
3. La marge d'erreur : chaque modèle a une marge d'erreur, avec des variations non prévisibles. Dans l'exemple, cela peut être une maladie le jour de l'examen ou une canicule qui peut influer sur la concentration. Ces éléments imprévus sont pris en compte par cette marge d'erreur.

En pratique, si le « point de départ » est de 50/100 et que « l'effet de l'étude » est de 5 %, cela signifie que sans heure d'étude, la note prévue est de 50/100. Pour chaque heure d'étude, l'augmentation de la note est de 5 %. Ainsi, après 6 heures d'étude, la note prévue pourrait atteindre 80/100 (50/100 + [6 x 5 %]).

La relation entre plus de 2 éléments

Si la note est affectée non seulement par les heures d'étude, mais aussi par la quantité de sommeil de l'étudiant ou par le nombre de cours qu'il a suivis, c'est là que la régression linéaire multiple entre en jeu. Elle met en lumière comment tous ces éléments ensemble impactent la note. Cela revient à dessiner une ligne à travers un ensemble de points, mais dans un espace à plusieurs dimensions.

Cela repose sur la méthode des « moindres carrés ». Il faut imaginer plusieurs lignes différentes à travers les points sur le graphique. Pour chaque ligne, il y aura des écarts entre ce que la ligne prédit et ce que les points réels montrent. La méthode des moindres carrés dessine une ligne qui rend ces différences (ou « écarts ») aussi petites que possible.

Le calcul pour trouver le « point de départ » et « l'effet de l'étude » est l'application de formules établies qui tiennent compte de toutes les données — dans cet exemple, les heures d'étude et les notes obtenues.

Comment calculer la régression linéaire simplement ?

Le calcul mathématique est grandement simplifié grâce à ces outils dédiés. Voici comment procéder.

1. Collecter les données : s'assurer d'avoir des données propres et bien organisées, généralement sous forme de tableau avec des colonnes distinctes pour chaque variable.
2. Utiliser un logiciel ou une application : des outils comme Excel, Google Sheets ou des logiciels spécialisés (SPSS, R et Python) ont des fonctions intégrées pour la régression linéaire. Par exemple, dans Excel, la fonction DROITEREG donne directement la pente et l'ordonnée à l'origine d'une régression linéaire simple.
3. Interpréter les résultats : une fois la régression exécutée, il faut se concentrer sur les coefficients pour comprendre la relation entre les variables. Le coefficient indique comment la variable dépendante change pour une unité de changement dans la variable indépendante. Le R2 précise la proportion de la variance de la variable dépendante expliquée par les variables indépendantes.
4. Visualiser la ligne de régression : tracer la ligne de régression permet d'obtenir une représentation visuelle de la relation. C'est souvent plus intuitif et cela facilite la communication des résultats à ceux qui sont moins familiers avec la régression.

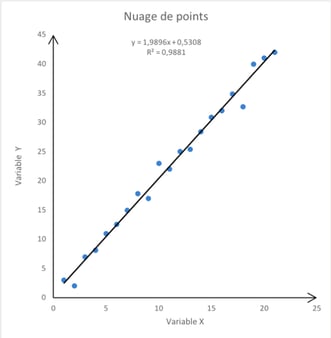
Source : Actuia

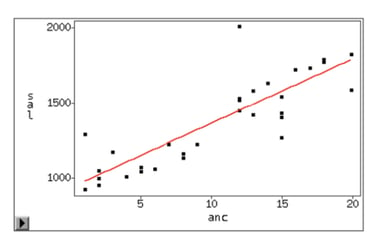
Source : Université de Toulouse

Comment interpréter les résultats d'une régression linéaire ?

Le résultat principal d'une régression linéaire est souvent présenté sous la forme d'un tableau de coefficients, accompagné d'un coefficient de détermination R2 et d'un test de Fisher.

Le tableau de coefficients

Il répertorie les paramètres estimés du modèle. Pour chaque variable, le tableau affiche :

• Le coefficient : la valeur estimée de l'effet de cette variable sur la variable dépendante.
• L'intervalle de confiance à 95 % : la plage dans laquelle on s'attend à ce que le coefficient réel réside, avec une confiance de 95 %.
• L'écart-type : la dispersion des coefficients estimés à partir de plusieurs échantillons.
• La statistique t : Un score qui indique à quel point chaque coefficient est éloigné de 0, en termes d'écarts-types.
• La p-valeur : la probabilité d'observer une statistique t aussi extrême si le coefficient réel était de 0 (c'est-à-dire, aucune relation).

Le coefficient de détermination R2

La fiabilité de la régression linéaire se mesure à l'aide du « coefficient de corrélation » R2, qui fait office d'indicateur de fiabilité :

• S'il est proche de 1 ou -1 : les données sont très fiables.
• S'il est proche de 0 : il n'existe pas vraiment de lien entre les éléments étudiés.

Il indique à quel point le modèle s'ajuste bien aux données observées. Pour affiner l'interprétation, le R2 ajusté prend en compte le nombre de variables dans le modèle, ce qui le rend utile pour comparer des modèles de complexités différentes.

Le test de Fisher

Il évalue la pertinence globale du modèle. Un ratio F élevé indique que le modèle est significatif par rapport à un modèle sans variables indépendantes. Sa p-valeur associée renseigne sur la probabilité de voir un tel ratio F si le modèle n'avait aucune pertinence.

Exemples de situations dans lesquelles utiliser la régression linéaire

La régression linéaire est employée dans une multitude de domaines pour étudier et prédire les comportements de certaines variables en fonction d'autres. Voici plusieurs exemples :

• L'impact des variables : la régression linéaire est couramment utilisée pour comprendre comment une ou plusieurs variables explicatives affectent une variable réponse. Par exemple, comment le prix d'un article affecte sa demande, comment le niveau d'éducation peut influencer le salaire ou comment des variations de température peuvent affecter la consommation d'énergie.
• Des prévisions : à partir des modèles de régression, il est possible de prévoir des résultats futurs. Ceci est pratique pour anticiper, par exemple, le chiffre d'affaires d'une entreprise en fonction de son budget de publicité, estimer le nombre de visiteurs sur un site web en se basant sur le nombre de mots-clés utilisés ou prévoir la durée de vie d'un produit basée sur son usage.
• Des tests d'hypothèses : un autre usage de la régression linéaire est qu'elle permet de tester des hypothèses spécifiques concernant les relations entre les variables, comme une entreprise qui peut tester si l'augmentation des dépenses publicitaires a réellement un impact positif significatif sur les ventes.
• Des optimisations : en entreprise, la régression linéaire est parfois utilisée pour optimiser certaines fonctions objectives, comme maximiser les profits tout en tenant compte du coût des matières premières ou minimiser le temps de trajet tout en considérant le trafic routier.

Pour aller plus loin dans votre stratégie commerciale, déterminez la rentabilité prévisionnelle de votre entreprise en téléchargeant le modèle de prévision des ventes, ou découvrez le logiciel de vente de HubSpot.