ANOVA est l'abréviation pour analyse de la variance, analysis of variance en anglais. Développée par le statisticien britannique Sir Ronald Aylmer Fisher au début du XXème siècle, ANOVA regroupe des modèles statistiques, dont le test F, ou test de Fisher. La méthode ANOVA est utilisée pour étudier le rapport de dépendance d'une variable quantitative à une ou deux variables qualitatives.
Dans le cadre d'une étude marketing, par exemple, l'analyse de la variance peut être appliquée au taux d'ouverture de la newsletter. L'entreprise obtient un taux d'ouverture de 50 % ; cette donnée, pour être exploitée à des fins d'amélioration, doit être affinée. C'est à cet effet que l'équipe marketing utilise le test ANOVA. Il s'agit de déterminer si les facteurs de type âge, sexe ou encore secteur géographique influent sur le taux d'ouverture de la newsletter. Le tableau ANOVA met ou non en évidence un rapport de dépendance du taux d'ouverture au facteur âge, sexe ou secteur géographique : l'entreprise qui observe un rapport de dépendance du taux au facteur sexe en déduit que le contenu de la newsletter n'intéresse pas autant les femmes que les hommes. L'équipe marketing peut travailler sur cet aspect pour mieux satisfaire son audience.
C'est quoi le test ANOVA ?
Le test ANOVA est une succession de formules statistiques qui expérimente deux hypothèses. L'hypothèse nulle met en évidence l'égalité des moyennes : la variable qualitative n'a aucune influence sur la variable quantitative. L'hypothèse alternative permet de constater qu'une moyenne s'écarte significativement des autres.
Quand utiliser le test ANOVA ?
ANOVA teste l'homogénéité de la moyenne de la variable quantitative étudiée sur les différentes valeurs de la variable qualitative. L'analyse de la variance, si elle aboutit à un résultat éloigné de zéro, permet de rejeter l'hypothèse nulle : la variable qualitative influe effectivement sur la variable quantitative.
La méthode ANOVA est utilisée dans le cadre d'études quantitatives dans de nombreux domaines, pour tester ou vérifier des hypothèses. Illustrations :
- Dans l'exemple de la newsletter, l'équipe marketing collecte de nombreuses données relatives au taux d'ouverture. L'entreprise connaît notamment le secteur géographique et le sexe de chaque abonné à la newsletter. Le test ANOVA sur le facteur secteur géographique ne met pas de lien de dépendance en évidence : à Bordeaux, à Paris et au Havre, la moyenne est similaire. Le test ANOVA sur le facteur sexe en revanche fait apparaître un écart significatif : l'analyse de la variance lui permet d'identifier ce facteur d'influence.
- Une enquête nationale menée par un institut de sondages révèle que 60 % des Français sont équipés d'un téléviseur connecté. ANOCA permet de savoir si le facteur géographique et le niveau de revenus sont déterminants. D'une ville à l'autre, aucun écart de moyenne significatif n'est constaté. Les moyennes diffèrent en revanche dans une large mesure en fonction des revenus. L'analyse de la variance conclut ainsi à une corrélation entre le fait de posséder un téléviseur connecté et le niveau de revenus.
- Un établissement d'enseignement sportif étudie la performance de ses élèves pour l'améliorer. L'établissement s'attache à comparer les résultats sportifs de plusieurs groupes de candidats, chaque groupe suivant un régime alimentaire spécifique. Le test F aboutit à un rapport de variances proche de 1 : le facteur régime alimentaire n'impacte pas les résultats sportifs. L'établissement teste une autre hypothèse : la performance varie en fonction de la fréquence de l'entraînement. L'analyse de la variance vérifie cette seconde hypothèse.
Ces exemples sont des illustrations schématisées de la méthode ANOVA, dans sa version univariée. En réalité, le test de Fisher compare les variances non seulement entre les échantillons, mais aussi au sein des échantillons. Des tests avancés, en outre, permettent de réaliser des analyses multivariées, qui testent le rapport de dépendance d'une variable quantitative à plusieurs facteurs qualitatifs. Des outils de calcul automatique permettent d'obtenir les résultats de l'analyse de la variance sous forme de tableau aisément exploitable, l'utilisateur se contentant de renseigner ses données d'expérience.
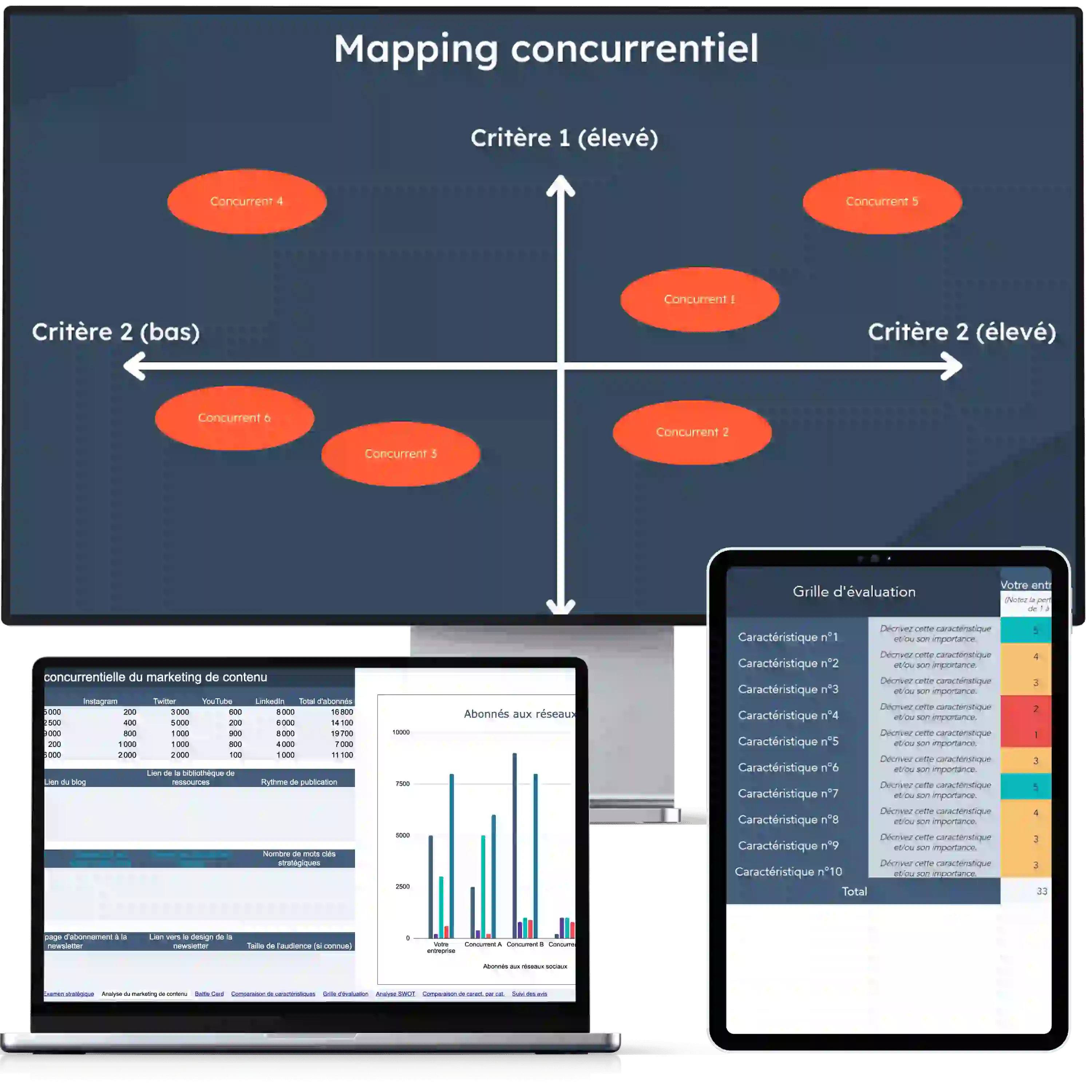
10 modèles d'analyse concurrentielle
Étudiez votre marché et vérifiez la viabilité des projets que vous comptez lancer.
- Mapping concurrentiel
- Analyse SWOT
- Examen stratégique
- Et bien d'autres
Télécharger
Tous les champs sont obligatoires.

Merci d'avoir soumis le formulaire
Cliquez sur le lien pour accéder au contenu en tout temps
Comment interpréter un tableau ANOVA ?
Le tableau ANOVA est le résultat final d'une succession de formules de calcul complexes. Il présente trois types de données numériques exploitables :
- Les degrés de liberté ou ddl.
- Le résultat noté F.
- La signification notée p : cette valeur, obtenue grâce aux données ddl et F, constitue le rapport de variance qui confirme ou qui infirme l'hypothèse testée. Si la valeur de p est inférieure à 0,05, l'hypothèse nulle, selon laquelle les moyennes sont égales, peut être vraisemblablement rejetée. C'est-à-dire que les variables qualitatives ont un effet significatif sur la variable quantitative : une moyenne au moins se distingue dans une large mesure au sein de l'échantillon.
Pour aller plus loin, effectuez une analyse SWOT, un battle card, un mapping concurrentiel ou une grille d'évaluation en téléchargeant les modèles d'analyse concurrentielle, ou découvrez le logiciel marketing de HubSpot.
Étude de marché






-68.png)


-47.png)



